可验证计算
可扩展性是目前区块链技术的主要瓶颈,如何扩容也是区块链技术的研究热点。 导致区块链可扩展性差的一个主要因素是单节点的处理能力有限,而且每笔交易都需要各节点验证计算。
PlatON基于可验证计算(VC)密码学算法(目前版本基于zk-SNARK)实现一种可验证合约的解决方案,主要思想是用户将复杂合约的计算外包给第三方,第三方具有强大的计算处理能力,他的计算成本低于用户自己直接计算的成本, 计算后,将结果和相应的计算正确证明上链验证,验证计算的速度成本都远低于直接计算,这样就可以扩展单节点的计算能力,而且不损失安全性。
zk-SNARK介绍#
zk-SNARK是“zero knowledge Succinct Non-interactive ARgument of Knowledge”的缩写,这一长串名字的主体是“argument of knowledge”,即“知情证明”,也就是掌握某事内幕的证据。修饰主体名词的定语由三部分组成,分别代表了此技术要解决的三个问题,分别是:
- zero knowledge:零知识,即在证明的过程中不透露任何内情;
- succinct:简洁的,主要是指验证过程不涉及大量数据传输以及验证算法简单;
- non-interactive:无交互。最初的版本是在证明者和验证者之间进行大量的交互才能完成证明,最新版本通过设置公共可信区域减少了大量交互
zk-SNARK是如何工作的#
将目标问题转化为二次计算方程(QAP)#
例如求解 $x^3+x+5=35$ 假设Alice知道x=3是解,但不想泄露给Bob,同时又要证明她知道这个方程式的解。
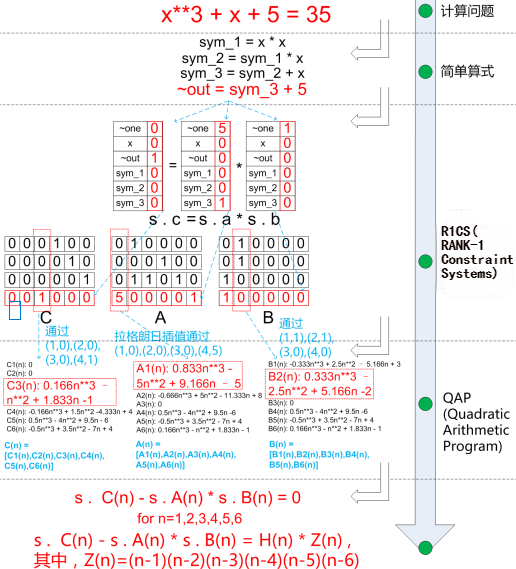
解决过程如下:
将计算方程拍平转化为各种简单算式(类似电路的逻辑门)
将简单算式转化为一级约束系统(R1CS)
一个 R1CS 是一组三维向量$(a, b, c)$构成的一个序列。假设R1CS的解是一个向量$s$,那么$s$必须满足这个等式: $s\cdot a\times s\cdot b - s\cdot c = 0$。这里的 $\cdot$ 代表向量的点乘,$a$、$b$ 和 $c$ 是其系数向量。依次完成所有简单算式的转化,将系数向量分别顺序排列,便得到A、B和C三个矩阵。
每个逻辑门对应一个gadget,gadget里面定义了相应的约束和产生证明witeness方法,我们也可以定制复杂逻辑门,例如mod,compare等运算,可以由多个约束组成。
每个向量的长度等于这个系统中所有变量的个数,同时也包括代表1的变量 ~one,我们把它放在向量第一个索引位置;还包括代表输出的 ~out,以及中间变量(上面的 $sym_1, sym_2, sym_3$)。这些向量通常比较稀疏,只在逻辑门相关的变量位置才有值,其他地方都为0。
上图中向量 $s$ 即可映射为: [~one, x, ~out, $sym_1, sym_2, sym_3$]
满足所有约束条件的向量 $s$ 就是问题的解,也就是witness: [1, 3, 35, 9, 27, 30]
- 将
R1CS转化为QAP
根据上面获得的$A$,$B$,$C$矩阵,通过拉格朗日插值的方式得到$A$,$B$,$C$的插值多项式表示$A(n)$,$B(n)$,$C(n)$ 。
求得多项式向量$A(n)$、$B(n)$和$C(n)$后,计算问题便转换为求取解向量 $s$ ,使得等式 $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=0$ 在 $n = 1,2,3,4,5,6$ 时成立,等价于: $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n)*Z(n)$,其中, $Z(n) = (n-1)(n-2)(n-3)(n-4)(n-5)(n-6)$。
抽样实现简洁验证#
上面完成一系列转化后,问题求解,就变成求解满足等式方程 $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n)*Z(n)$ 的解。
Alice 可以用她知道的解 $s$ ,计算多项式 $P(n)$ 和 $H(n) = P(n)/Z(n)$,然后将两个多项式 $P(n)$、$H(n)$ 发给验证者 Bob。后者通过检查 $P(n) ?= H(n) * Z(n)$ 是否成立来判断 Alice 是否真的知道解。
这种方式没有泄露 $s$ ,但由于多项式的度往往比较大,导致传输和计算非常耗时,实际不可取,当然还有一个因数是没法确定 $P(n)$ 是由 $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)$ 组成。因此除了不泄露解,还需要让验证的时候更简洁。zk-SNARK采用抽样验证的方式简化验证,即 Bob 随机选择一个 $t$,发送给 Alice,计算出 $P(t)$,$H(t)$ 的值,将值传给 Bob 验证。过程如下所示:
- Bob 任意选择一个点 $n = t$ 发给 Alice ,这个点称为抽样点
- Alice 计算 $P(t)$ 和 $H(t)$
- Alice $P(t)$ 和 $H(t)$ 发还给Bob
- Bob 检查 $P(t) ?= H(t)\times Z(t)$
这种验证方式,Bob 可以大概率确定 Alice 知道解,之所以大概率是 Alice 存在一种可能,知道另一个解,使得 $P(t)=H(t)\times Z(t)$ 成立,但这个概率是非常小的。假设$A$,$B$,$C$ 的度为$d$,则 $p(n)$ 的度为 $2d$,两个不等价的多项式交点数量最多只有 $2d$ 个,$2d$ 相较于有限域的元素个数$n$ 来说很小的情况下,Alice 随意选择t使多项式 $P(x)$ 被校验通过的概率只有 $2d/n$。
同态隐藏#
由于暴露了 $t$ 给 Alice ,Alice 同样可以构造 $P'(t)$ , $H'(t)$ 使得 $H'(t) = P'(t)/Z(t)$ 成立。因此抽样点 $t$ 不能让 Prover(Alice)知道,同时还得让 Prover 能给出抽样点处的值,zk-SNARK是通过同态隐藏的方式做到这一点的。
“同态隐藏”是输入 $x$ 到输出 $X$ 的某种映射(mapping)$E$ 的特性:
- 对于绝大多数的$ x$,已知 $X=E(x)$ ,无法推导出 $x$ ;
- 如果$x_1\neq x_2$ ,则 $E(x_1)\neq E(x_2)$;
- $E(ax_1+bx_2)=a * E(x_1)+b * E(x_2)$
Bob 不再直接将抽样点告知 Alice,而是提供了 $t$ 的一系列指数 $t0、t1、t2、t3...tN$ 的映射值 $E(1)、E(t1)、E(t2)、E(t3)...E(tN)$,如下所示:
- Bob 计算 $E(1)、E(t1)、E(t2)、E(t3)...E(tN)$ 发给 Alice;
- Alice 计算 $E(P(t))$ 和 $E(H(t))$;
- Alice 把 $E(P(t))$ 和 $E(H(t))$ 发还给 Bob;
- Bob 检查 $E(P(t)) ?= E(H(t))\times E(Z(t))$ ( $t$ 的值,Bob知道,因此可以算出 $z(t)=a$ ,从而算出$E(aH(t))$ )。
KCA#
假设 Prover 不知道使 $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n) * Z(n)$ 成立的解 $s$,但知道另一个问题的解 $s$: $s'\cdot C'(n)-s'\cdot A'(n) \times s'\cdot B'(n)=H'(n)*Z(n)$ 。Prover 便可用不同于原始问题的系数向量 $A'(n)$ 、$B'(n)$ 和 $C'(n)$ 来生成 $P'(n)=s\cdot C'(n)-s\cdot A'(n) * s\cdot B'(n)$ ,然后发给 Verifier 验证。 Verifier 如何才能知道 Prover 计算 $P(n)$ 使用的是不是规定的系数向量$A(n)$、$B(n)$ 和 $C(n)$ 呢?这一过程便称为KCA(Knowledge of Coefficient Test and Assumption)。原理如下:
先定义:
$\alpha$ 是指满足$b=\alpha * a$ 的一对值$(a,b)$,乘法($*$)是椭圆曲线乘法, 具备两个特性:
- 当$\alpha$ 值很大的情况下,很难通过 $a$ 和$b$倒推出$\alpha$;
- 加法和乘法满足可交换群的特性。
我们利用 $\alpha对$ 的特性,构建一个称为KCA(Knowledge of Coefficient Test and Assumption)的过程:
- B 随机选择一个 对 值生成 $\alpha$ 对$(a,b)$,自己保存 $\alpha$ 值,α 对$(a,b)$发送给 A;
- A 选择$\lambda$,生成 $(a',b')=(\lambda \cdot a, \lambda \cdot b)$,把$(a',b')$回传给B。利用交换律,可以证明$(a',b')$也是一个 $\alpha$对:$b' = \lambda \cdot b = \lambda \alpha \cdot a = \alpha (\lambda \cdot a) = \alpha \cdot a'$;
- B 校验 $(a',b')$ ,证实是 $\alpha$ 对,就可以断言 A 知道$\lambda$。
推广到多个d-KCA:
- B 发送一系列的 $\alpha$ 对给 A;
- A 使用 $(a',b')=(c_1\cdot a_1+c_2\cdot a_2,c_1\cdot b_1+c_2\cdot b_2)$ 生成新的 $\alpha$ 对;
- B 验证通过,可以断言 A 知道 $c$ 数组。
回到开始的问题:Prover(Alice)可以构造和 $A(n)$、$B(n)$ 和 $C(n)$ 无关的多项式 $P'(n)$ 来满足等式,因此我们可以在上一节的例子中改进为,Bob 只将 $E(A(t))$,$E(B(t))$,$E(C(t))$ 的值发送给 Alice,Alice 只能基于这些值构建 $E(P(t))$ 。
双线性映射(bilinear map):乘法的同态隐藏#
在上面的KCA验证中,需要验证 $E(\alpha A(t)) = \alpha E(A(t))$ 涉及到乘法运算,而 $\alpha$ 在构建可信参数的时候已经被丢弃,所以如果想做到乘法的同态隐藏了,那就需要用到双线性映射。
上面介绍的同态隐藏是一对一的,即将一个输入映射到一个输出。而双线性映射是将分别来自两个域的两个元素映射到第三个域中的一个元素:$e(X, Y) \rightarrow Z$,同时在两个输入上都具备线性:
$e(P+R, Q) = e(P, Q) + e(R, Q) e(P, Q+S) = e(P, Q) + e(P, S)$
假设对于 $x$ 的任意两种因数分解 $(a, b)$ 和 $(c, d)$(即$x=ab=cd$),存在两个加法同态映射 $E1$ 和 $E2$,以及一个双线性映射 $e$,使得以下等式总是成立:
$e(E_1(a), E_2(b)) = e(E_1(c), E_2(d)) = X$
那么,$x\rightarrow X$ 的映射也是加法同态映射。
由上我们得出了乘法的同态隐藏公式:
$E(xy) = e(E_1(x), E_2(y))$
根据如上公式,为了验证 $\pi_A' ?=\alpha \pi_A$, 我们可以转化为验证 $e(\pi_A, E_2(\alpha)) ?= e(\pi_A', E_2(1))$ (B,C同理)。
零交互#
在上面的例子中,我们需要Bob发送大量的 $E(A(t))$,$E(B(t))$,$E(C(t))$ 序列给 Alice,这个数据量是非常巨大的,传输很耗时,也不够简洁,如何解决这一问题: zk-SNARK把 Bob 发给 Alice 的一大坨数据 $E(A(t))$,$E(B(t))$,$E(C(t))$ 变成所谓的“共同参考数据集”(CRS,Common Reference String),通过某种可信的方式产生,作为一种全体节点的共识,在所有交易的验证过程中使用,因而“质询-响应”的交互式验证方式变成了只需要 Proof 提交证据即可。
可验证合约#
PlatON的VC架构图#

- vc-contract template:用户根据提供的模板编写 vc 合约,可以输入任意计算模型,主要实现三个接口:
- compute():计算请求
- real_compute() :生成计算结果和证明
- set_result():验证计算结果和证明
- vclang:将用户编写的 vc 合约编译,生成 wasm vm 支持的执行文件,合约开发者无需关心具体的 libsnark api 使用方法,只需编写好自己的计算模型代码即可
- vcc-reslover:在wasm虚拟机中预置支持访问 libcsnark api 的接口层,以 c-go 的方式调用 libcsnark 接口
- libcsnark:封装 libsnark api,将 c++ 实现的 libsnark 可以由 c 接口访问
- vc_pool:负责 vc 的交易处理,分发 vc 计算任务,并将计算结果和证明上链
可验证合约编译#
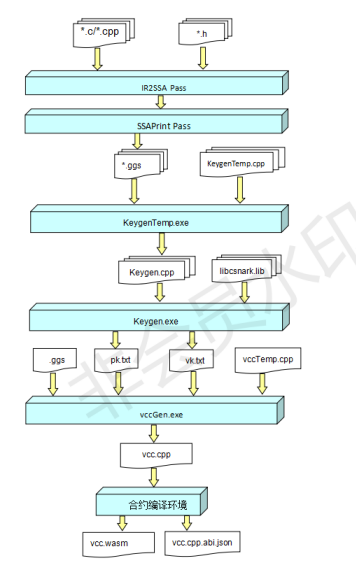
- 将用户程序编译生成的IR序列,转化为SSA,最终转化为 libcsnark 支持的 gadget 表示 ggs
- 将ggs,和keygenTemp.cpp,结合生成keygen
- vclang 通过 keygen 生成 pk,vk(CRS构建),这个过程会进行大量的椭圆曲线乘法运算,产生pk,vk之后序列化至合约模板中,pk是用来生成证明的可信参数,vk 是验证用到的可信参数
- vclang 再将 pk,vk 序列化至 vccTemp.cpp 中生成 vcc.cpp
- vclang 编译生成 vcc.cpp 生成 vcc.wasm
可验证合约是如何工作的#
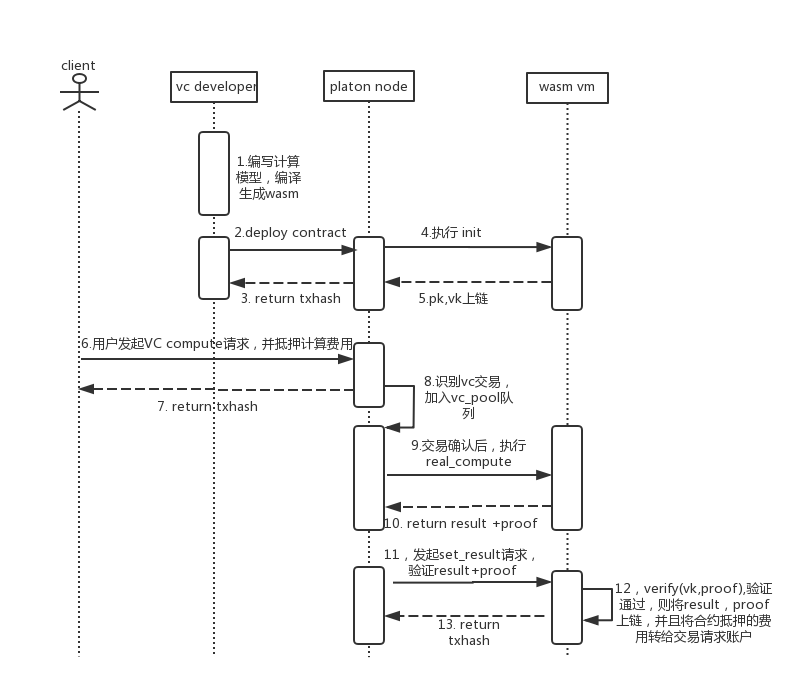
主要过程说明:
- 合约编译之后,已经生成了 $pk$,$vk$,部署至 PlatON 网络之后,$pk$,$vk$ 存储至链上,无法被篡改,可方便节点访问。
- 当 vc compute 交易执行时,会创建一个 vc task,taskid 由 tx 的 nonce 组成,并以 taskid 为 key,存储输入参数 $x$。
- compute交易写入区块之后,会触发 vc_pool解析交易event,从而决定是否将task加入vc_pool的队列中
- 等待20个区块确认之后,就可以开始执行 real_compute,由于是链下计算,不会产生交易费用。real_compute 的过程是首先根据执行此前编译生成的 gadget 序列运算产生
s(witness),一旦计算出 $s$,就可以根据pk,计算出证明 $\pi_A$, $\pi_B$, $\pi_C$等系列,即是 proof。 set_result(proof, result)是将计算结果和证明上链,该过程主要是verify(vk, proof, input),一旦验证通过,则交易发起者可获取计算酬劳。zk-SNARK的 verify 的时间相对产生 proof 的阶段比较短,但也是和输入参数长度相关,所以需要注意限制输入参数长度,防止该笔交易的gas费用过高,增加验证者成本。
合约的激励模型#
有计算外包需要的用户,需要先抵押合适费用至合约账户,platon各节点可自行竞争计算任务,一旦计算成功,生成结果和证明,就发起set_result交易请求,需要计算节点先支付该笔交易的矿工费,节点收到请求,执行set_result,一旦验证通过交易中携带的 proof 和 result 参数,则认为交易请求者成功计算出结果,会将合约账户抵押的费用转账至请求者账户中,失败则不会给以激励。
方案分析#
性能分析#
| 运算阶段 | 运算 | 用户 | 计算节点 |
|---|---|---|---|
| keygen构建 | 指数 | O(m+n) | 0 |
| real_compute | 指数 | 0 | O(m) |
| set_result | 双线性配对运算 ,指数 | O(1),O(n) | 0 |
m 为 $A$,$B$,$C$ 多项式的度,$n$ 为输入参数长度
- keygen构建:将抽样值进行同态隐藏生成可信参数,由于 m 往往较大,而且是指数运算,时间也比较长,但该过程是在合约编译阶段进行,所以不会影响合约运行阶段性能
- real_compute :需要做 $O(m)$ 次的指数运算生成 witness 和 proof,该过程可以分发至链下第三方进行快速运算
- set_result :verify 根据输入生成 proof 的组成部分,需要 $o(n)$ 次指数运算,然后使用固定次数双线性配对运算做验证,该过程是在链上完成,因此需要优化其执行时间,确保在一个可接受的计算成本范围
性能对比#
| time(Setup) | key len(Setup) | time(Proving) | memory(Proving) | time(Verifying) | proof len(Verifying) | |
|---|---|---|---|---|---|---|
| zk-SNARK | ~28min | ~18GB | ~18min | ~216GB | <10ms | 230B |
| zk-SNARK(Zcash-Sprout) | ~27hr(6 player) | ~900MB | ~37s | ~1.5GB | <10ms | ~300B |
| zk-SNARK(Zcash-Sapling) | months-MPC | <800MB | ~7s | ~40MB | <10ms | ~200B |
| zk-STARK | <0.0.1s | 16B | 6min | 131GB | ~0.1s | ~1.2MB |
| Bulletproof | 2min | ~1MB | ~3s | ~1.5KB | ||
| ZKBoo() | ~33ms | ~MBs | ~38ms | ~200KB | ||
| Ligero() | ~140ms | ~MBs | ~60ms | ~34KB |
后续规划#
PlatON后续实现更优化的VC算法,在以下几方面进行优化:
- 去掉SNARK的ZK属性提高性能,降低生成证明时间和验证时间
- 结合多方安全计算(MPC)和同态加密(HE)来实现隐私计算
- 考虑采用更优化的椭圆曲线优化椭圆曲线加密的运算速度
- 优化验证处理:预处理双曲线配对运算,预置中间值,无需重复计算
- 采用MPC等算法保证 Setup 过程的安全性