Verifiable Computation

Scalability is the key bottleneck for current blockchain technology to hinder it from being adopted by large-scale applications. In view of this, more and more blockchain researchers are working on scalability solutions. One of the main factors resulting in its poor scalability is the limited processing ability for a single node. Besides, every newly generated transaction will be executed repeatedly by every single node on blockchain to validate its legitimacy, which severely impedes the efficiency of blockchain.

PlatON builds a scalability solution called verifiable smart contract which is implemented by verifiable computing (VC) cryptography algorithm (currently based on zkSNARK). The whole idea is outsourcing complex computing contracts to third parties that possess more computing power than those who issue the computing tasks. After finishing executing the computing task, the output result and the corresponding correctness proof will be stored on-chain. And then every node that would like to utilize the output result can simply verify the correctness proof before getting the output result, which means there is no need to execute the computing task directly that takes more cost than verifying the proof. By means of this, more computing contract tasks are able to be processed by a single node without loss of security.

Introduction to zkSNARK#

zkSNARK, which abbreviates from "zero- knowledge Succinct Non-interactive ARgument of Knowledge", is one kind of zero knowledge proof cryptographic primitives. It is a method that one party can prove to another party that he knows the secret knowledge without revealing it. As claimed by its name, three things it solves are:

Zero-knowledge: No additional information would be revealed during the process of verifying.
Succinct: No need to convey any information apart from the secret knowledge itself, and it can be verified easily.
Non-interactive: To verify the proof, amounts of interactions between prover and verifier are required. In the newly zkSNARK construction, it can be reduced by setting up a public trusted zone.

How it works#

Transforming the target problem into Quadratic Arithmetic Program (QAP)#

For example, get the solution of the equation $x^3+x+5=35$. Suppose Alice knows the solution is $x=3$, but she doesn't want to reveal it to Bob while proving to him that she does know it.

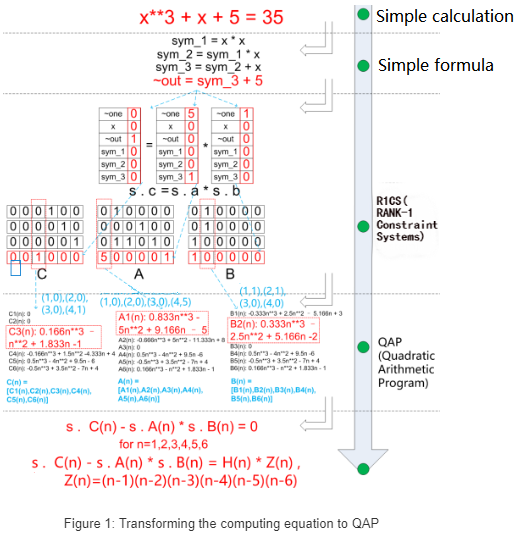
\ Referring to Vitalik's blog^[1], it can be solved as follows:

Alice transforms the computing equation to the basic arithmetics (can be seen as the logic gates in circuits).
Alice converts the basic arithmetics to the Rank-1 Constraint Systems (R1CS).
The R1CS is a sequence combined with the vectors $(a,b,c)$. Suppose the solution of this R1CS is vector $s$, then it must satisfy the equation $s\cdot a\times s\cdot b - s\cdot c = 0$, where $\cdot$ is the multiplication between vectors and $a,b,c$ are the vector of coefficients. Completing the conversion of all basic arithmetics, and arrange the coefficients vector in order, then obtain three final matrices $A$,$B$ and $C$.

Each logic gate is corresponding to a gadget, in which defines the constraints and the method of generating witness. And we can also customize complex logic gate, such as $mod$, $compare$, $etc$, which can consist of multiple constraints.

The length of each vector is equal to the numbers of all variables in this system, in which include the variable ~one put at the first index position representing 1, and the variable ~out representing the output, and some intermediate variables $sym_1, sym_2, sym_3$ as shown in Figure 1. Generally, these vectors are sparse and only of which are at the logical gate-related variable positions would be assigned the value, and all the left positions would be assigned 0.

The vector $s$ in Figure 1 can be mapped to [~one, x, ~out, sym_1, sym_2, sym_3], the one that satisfies all constraint conditions is the solution of the computing equation, and it's the so-called $witness$, which equals to [1,3,35,9,27,30].

Transforming R1CS to QAP.

With obtained three matrices $A$, $B$, and $C$ in the previous step, we are able to get polynomials $A(n)$, $B(n)$ and $C(n)$ responding $A$, $B$, and $C$ respectively by the Lagrangian interpolation. Then the computing equation can be reduced to obtain a vector $s$, which satisfies $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=0$ when $n=1,2,3,4,5,6$ respectively. And it is equivalent to satisfy the equation $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n)*Z(n)$, where $Z(n)=(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)$.

Sampling for succint verification#

After completing a series of transformations above, the computing equation is reduced to obtain the solution of the new equation $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n)*Z(n)$.

Alice can use the solution $s$ she already knows to compute polynomials $P(n)$ and $H(n) = P(n)/Z(n)$, and then sends $P(n)$ and $H(n)$ to the verifier Bob. When Bob succeeds receiving both two of them, he would tell that Alice does know the solution by checking whether $P(n)$ equals to $H(n)*Z(n)$ or not.

$s$ is not leaked by this means, but since the degree of polynomial tends to be pretty large, resulting ineffective time cost for transmitting and computing to make it impractical, and another reason is that it cannot be guaranteed $P(n)$ consists of $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)$.

Therefore, the solution cannot be leaked not only, but also can be verified succinctly. zkSNARK takes the way of sampling verification to simply the verification process, i.e., Bob randomly selects $t$, then sends it to Alice. Alice computes $P(t)$ and $H(t)$, and sends them back to Bob to be verified. The processes are shown below:

Bob randomly select a point $n=t$, which called the sampling point, then sends it to Alice;
Alice computes $P(t)$ and $H(t)$;
Alice sends back $P(t)$ and $H(t)$ to Bob;
Bob checks whether $P(t)$ is equal to $H(t)\times Z(t)$ or not.

By this mean of verification, Bob can assure Alice knows the solution with high probability. Since it has a little probability that there is another solution satisfying $P(t)=H(t)\times Z(t)$, it cannot be 100 percent guaranteed Alice knows the solution. Suppose the degree of $A$, $B$ and $C$ is $d$, then the degree of $p(n)$ is $2d$ and the number of intersections of two inequality polynomials is $2d$ at most, which is very small compared to the number of elements $n$ in the finite field, and the probability is only $2d/n$ if $t$ randomly selected by Alice can make $P(x)$ be validated.

Homomorphic hiding#

Since $t$ is revealed to Alice, she can also construct P'(t), H'(t) such that H'(t) = P'(t)/Z(t) holds. Then the sampling point $t$ should be hidden from the prover Alice while making she knows it. zkSNARK can do this by homomorphic hiding.

"Homomorphic Hiding" is a property of the mapping $E$ from input $x$ to output $X$:

For most $x$, given $X=E(x)$, $x$ cannot be deduced vice versa;
If $x_1\neq x_2$, then $E(x_1)\neq E(x_2)$;
$E(ax_1+bx_2) = a * E(x_1) + b * E(x_2)$.

Instead of informing Alice the sampling point directly, Bob provides a sequence of mapping values $ E(t_1), E(t_2), E(t_3),..., E(t_N)$ from input $t_0, t_1, t_2, t_3, ..., t_n$ respectively. The processing steps are listed below:

Bob computes $ E(t_1), E(t_2), E(t_3),..., E(t_N)$, and sends all of them to Alice;
Alice computes $E(P(t))$ and $E(H(t))$;
Alice sends back $E(P(t)$ and $E(H(t))$ to Bob;
Bob checks whether $E(P(t))$ is equal to $E(H(t))\times E(Z(t))$ or not. (since Bob knows $t$, he can compute $z(t)=a$, and obtain $E(aH(t))$).

KCA#

Suppose the prover doesn't know the solution $s$ satisfying $s\cdot C(n)-s\cdot A(n) \times s\cdot B(n)=H(n) * Z(n)$, but she knows another solution $s'$ satifying $s'\cdot C'(n)-s'\cdot A'(n) \times s'\cdot B'(n)=H'(n)*Z(n)$. Then the prover can use the coefficient vectors $A'(n)$, $B'(n)$ and $C'(n)$ to compute $P'(n)=s\cdot C'(n)-s\cdot A'(n) * s\cdot B'(n)$, then it would be sent to the verifier to get verified. How can the verifier knows the prover computes $P(n)$ does use the difined coefficient vectors $A(n)$, $B(n)$ and $C(n)$? The whole process is Knowledge of Coefficient Test and Assumption, which abbreviated by KCA. The details of KCA are described below.

Firstly, we define $\alpha$ is the pair of $(a,b)$ satisfying $b=\alpha * a$, where $*$ is the multiplication operation on Elliptic Curves, meeting two properties:

If $\alpha$ is big enough, it is nearly impossible to compute $\alpha$ from $a$ and $b$;
Addition and multiplication operations satisfy the characteristics of commutative groups.

We utilize the properties of $\alpha$ to construct a process called KCA (Knowledge of Coefficient Test and Assumption):

Bob randomly selects $\alpha$ and generates pair $(a,b)$, he saves $\alpha$, but sends $(a,b)$ to Alice;
Alice selects $\lambda$ and generates new pair $(a',b')=(\lambda \cdot a, \lambda \cdot b)$, then returns $(a',b')$ to Bob. With the commutative formula, it can be proved that $(a', b')$ is also a $\alpha$ pair: $b' = \lambda \cdot b = \lambda \alpha \cdot a = \alpha (\lambda \cdot a) = \alpha \cdot a'$;
Bob check if $(a',b')$ is a $\alpha$ pair, if yes, it can be claimed Alice knows $\lambda$.

Extending to the conditions of multiple KCA:

Bob sends a sequence of pair $\alpha$ to Alice;
Alice applys $(a',b')=(c_1\cdot a_1+c_2\cdot a_2,c_1\cdot b_1+c_2\cdot b_2)$ to generate a newly $\alpha$ pair;
If Bob validates that $(a',b')$ is a $\alpha$ pair, it can be claimed Alice knows array $c=[c_1,c_2]$.

Back to the beginning: the prover Alice can construct polynomials $P'(n)$ that are independent of $A(n)$, $B(n)$ and $C(n)$ to satisfy the equation, so we can modify the example in the previous section to a new one, where Bob only sends $E(A(t))$, $E(B(t))$ and $E(C(t))$ to Alice. Only based on them, Alice is able to construct $E(P(t))$.

Bilinear map: homomorphic hiding of multiplication#

In the KCA verification described above, it involves multiplication in order to verify $E(\alpha A(t)) = \alpha E(A(t))$, while $\alpha$ is deprecated when constructing the trusted parameters. So bilinear map is acquired to make the homomorphic hiding for multiplication.

The homomorphic hiding described above is one-to-one, i.e., mapping an input to an output. A bilinear map maps two elements from two responding fields to an element in the third field: $e(X, Y) \rightarrow Z$, and has linearity property on both inputs:

$e(P+R, Q) = e(P, Q) + e(R, Q) e(P, Q+S) = e(P, Q) + e(P, S)$

Suppose that $(a, b)$ and $(c, d)$ are two different factorizations of $x$ (i.e. $x = ab = cd$), there are two additive homomorphic maps $E_1$ and $E_2$, and a bilinear map $e$, such that The equation below is always true:

$e(E_1(a), E_2(b)) = e(E_1(c), E_2(d)) = X$

Then, the map of $x\rightarrow X$ is also an additive homomorphic map.

From the above we have derived the homomorphic hiding formula of multiplication:

$E(xy) = e(E_1(x), E_2(y))$

According to the formula above, in order to verify $\pi_A' ?=\alpha \pi_A$, we can convert it to verify $e(\pi_A, E_2(\alpha)) ?= e(\pi_A', E_2(1))$ (B, C is in the same way).

None interaction#

In the example above, Bob need to send amounts of sequences of $E(A(t))$, $E(B(t))$ and $E(C(t))$ to Alice, where the sequence data is pretty massive, and is time-consuming during the transmitting process, and also is not simply enough. Here is the solution: zkSNARK packs punch of data $E(A(t))$, $E(B(t))$ and $E(C(t))$ that Bob sent to Alice to the so-called Common Reference String (CRS), which is generated by a kind of trusted way, and used in the process of all of transaction verification as the consensus of all nodes. Therefore, the verification way is changed from an interactive "request-response" way to the way of simply submitting a proof.

Verifiable contract#

Figure 2: The VC architect in PlatON

\ The workflow of VC in PlatON is:

vc-contract template: The user codes the vc contract according to the provided template, and any computing model can be implemented, mainly implementing three interfaces:
1. Compute(): Initiate the computing request
2. Real_compute(): Generate computing results and proof
3. Set_result(): verify the results and proof
vclang: The vclang compiles the vc contract into the executable file supported by wasm vm. There is no need to care about the specific libsnark api usage method for developers, just only to code their own computing model.
vcc-reslover: The vcc-resolver presets the interface layer that supports access to the libcsnark api in the wasm virtual machine, and invokes the libcsnark interface in c-go mode.
Libcsnark: The Libcsnark encapsulates libsnark api, making it accessible for C interface with the implemented libsnark by C++.
vc_pool: The vc_pool is responsible for processing vc transaction, distributing vc computing tasks and putting computing results and proofs onto the blockchain.

Compiling verifiable contract#

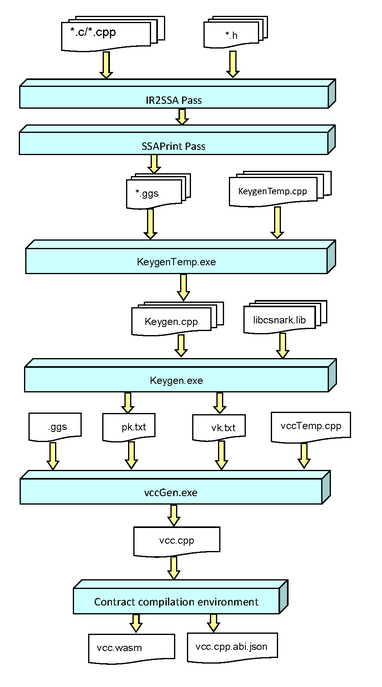
vclang

Figure 3: Compiling verifiable contract to WASM

\ The processes of compling verifiable contract are:

The vc compiler compiles the contract coded by users to IRs, and then converted to SSA, finally, it would be transformed into ggs, which is the gadget representation supported by libcsnark.
Combines gss and keygenTemp.cpp to generate keygen.
The vclang generates $pk$ and $vk$ (CRS construction) by keygen. This process performs a large number of elliptic curve multiplication operations, and after finishing generating $pk$ and $vk$, both of them would be serialized into the contract template, where $pk$ is used to generate trusted parameters, and $vk$ is the trusted parameter for verification.
The vclang serializes $pk$ and $vk$ into vccTemp.cpp to generate vcc.cpp.
The vclang compiles vcc.cpp to obtain vcc.wasm.

How it works#

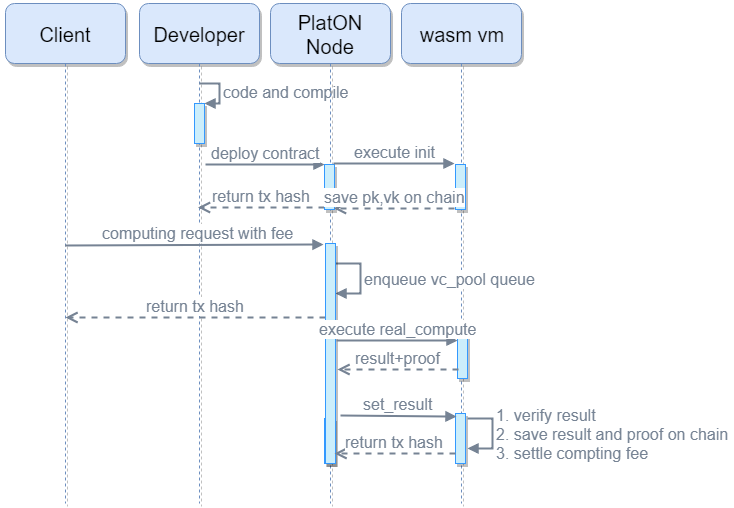
vc-work

Figure 4: The workflow of verifiable contract

\ Here is the workflow of verifiable contract:

After finishing compiling the contract, $pk$ and $vk$ would be obtained and would be deployed onto PlatON for storge to make them accessible to other nodes, and from being tampered.
When executes the vc compute transaction, a vc task would be created, which is combined with nonce of the transaction and the input parameter x corresponding its key taskid.
Once the compute transaction succeed being confirmed, the transaction parsing event would be invoked by the vc pool to check whether this task could be added to the vc pool or not.
Waiting for 20 blocks confirmation, it starts to execute real_compute, which is off-chain computation making it no fee cost. The processes of real_compute are two steps. Firstly, computing the witness $s$ according to the obtained gadget sequence in the previous compilation. Secondly, with the additional pk got in step 1, the computing node can generate the final proof, which is a sequence of proofs combined with $\pi_A$, $\pi_B$, $\pi_C$, etc.
The result and proof are deployed onto PlatON by Set_result(proof,result), which is mainly executing verify (vk,proof,input). Once validated, the transaction initiator would be rewarded for its computing contribution. The verify time of zkSNARK is relatively short compared to the time of proof generation, but it is also related to the length of the input parameter, so it is necessary to pay attention to limiting the length of the input parameter, preventing the gas cost of the transaction from being too high, and increasing the cost of the verifier.

The incentive mechanism of verifiable contract#

Users who have the requirement to outsource their computation need to mortgage the appropriate fees to the contract. Each node in the PlatON network can compete for the computing task. Once the computing node succeeds in finishing the computing task and obtain the result and the corresponding proof, the set_result transaction request would be initiated after that the computing node finished paying the miner fee. As the verifying node receives this request, the set_result would be executed in the meantime, and the proof and result parameters encapsulated in the transaction would be validated their legitimacy. If yes, it could be considered that the computing node obtains the correct result. Meanwhile, the mortgage fee would be transferred to the requester's account as the incentive, and no incentive would be offered if fails.

Analysis to the VC solution#

Performance analysis#

computing stage	operation	user	computing node
keygen construction	exponential	O(m+n)	0
real_compute	exponential	0	O(m)
set_result	hyperbolic matching operation, exponential	O(1),O(n)	0

where $m$ is the degree of polynomials $A$,$B$ and $C$, $n$ is the length of input parameter.

keygen construction: homomorphic hiding the sampled value to generate trusted parameters. Since $m$ is a large number commonly, and it is an exponential operation, then it would take a relatively long time. As this process is done after compiling the contract, it would not affect the performance of contract executing.
real_compute: $O(m)$ times of exponential operations are required to generate the witness and proof. And this can be distributed to third parties for fast computation.
set_result: According to the specific input, the verify process generate parts of the proof, requiring $O(n)$ times of operations, and then take the fixed hyperbolic matching operation to make the verification. Since this process is done on-chain, it needs to be optimized to assure it at an acceptable computing cost.

Comparison of different VC technologies#

	time(Setup)	key len(Setup)	time(Proving)	memory(Proving)	time(Verifying)	proof len(Verifying)
zkSNARK	~28min	~18GB	~18min	~216GB	<10ms	230B
zkSNARK(Zcash-Sprout)	~27hr(6 player)	~900MB	~37s	~1.5GB	<10ms	~300B
zkSNARK(Zcash-Sapling)	months-MPC	<800MB	~7s	~40MB	<10ms	~200B
zkSTARK	<0.1s	16B	6min	131GB	~0.1s	~1.2MB
Bulletproof			2min	~1MB	~3s	~1.5KB
ZKBoo()			~33ms	~MBs	~38ms	~200KB
Ligero()			~140ms	~MBs	~60ms	~34KB

Future plans#

PlatON will implement more optimized VC algorithm, it would be optimized in the following several ways:

Cutting the ZK property off from SNARK to improve its efficiency, decreases the proof generation and verification time.
Implementing privacy-preserving computing combining with MPC and HE.
Considering adopting more optimized elliptic curves to increase the speed of encryption on ECC.
Optimizing the verification process, including pre-processing the hyperbolic matching operation and presetting intermediate values to keep it from the repeated computation.
Adopting some algorithms like MPC to guarantee security during the process of Setup.

Reference#

[1]. https://vitalik.ca/