Skip to main content

Secure Multi Party Computation

With the Digital Era coming into our daily lives, we place great store in the value of data by the fact that it is regarded as the oil in this digital era. Because of that, massive important data belong to institutions or enterprises are kept stored in local from revealing to others. Blockchain as a decentralized network, allows everyone to join this network, especially for those who have the willingness to contribute to it. But the truth is, no important data would be put onto blockchain by the fact of its transparency property, which means any data on it can be seen by everyone. With the increasing number of data leaking issues nowadays, the public, mostly for those institutions holding amounts of data, also become to realize how important it is to protect the privacy of their own data.

Secure Multi-party Computation, abbreviated as MPC, allow multiple parties jointly compute a given function neither revealing their own input to others nor trusting a third party, which can leverage the value of data while protecting them from exposing. PlatON harnesses the power of MPC to facilitate the flowing of data by transforming application algorithms into secret contracts. The idea behind it is that MPC can transform application algorithms into secret contracts. Afterward, these secret contracts will be deployed onto blockchain, and can be invoked by data owners and computing power providers in this network. With more and more data related roles joining PlatON, it will be built into a privacy-preserving computing network that everyone can make their contributions to it eventually.

Introduction to MPC#

MPC is defined as the situation where $N$ parties can jointly compute a given function $f(x_1,\dots ,x_n)=y$ and receive the resulting output without ever exposing their responding secret input $x_1,x_2,\dots ,x_n$. When finishing this computation, the output result $y$ is equal to the computing result in the traditional way. Besides, no more additional information can be deduced from the output result itself.

The basic properties of MPC are:

  • input privacy: The intermediate data would not leak any information about original data during the process of MPC.
  • robustness: No incorrect result would be obtained when MPC computation is finished.

The typical paradigm of constructing a general MPC protocol is based on garbled circuit which was introduced by Andrew Chi-Chih Yao in 1986 for secure two-party computation. After that, it was extended to secure multi-party computation with the introduction of BMR protocol by Beaver, Micali and Rogaway. For now, protocols and algorithms related to MPC consist of Garbled Circuit, Oblivious Transfer, Secret Sharing, BGW, GMW, BMR, etc. As for the engineering implementation, many of them have already been open-soured, such as SPDZ, LEGO, Sharemind, Fairplay and so on. Combining Garbled Circuit (GC) with Oblivious Transfer (OT) can construct a general secure two-party computation framework.

Garbled Circuit#

The details of Garbled Circuit can be found on this web page.

Plenty of optimization solutions towards Garbled Circuit have been come up with, including Free-XOR, which means no XOR gate need to be encrypted, Row Reduction and Half Gate, which can reduce the number of ciphertext from 4 to 2 for AND gate. Very recent research result using Authenticated Garbled Circuit to achieve very efficient protocols for both two-party and multi-party case in the malicious model.

If you want to know deeper about Garbled Circuit, this paper is good for you.

Oblivious Transfer#

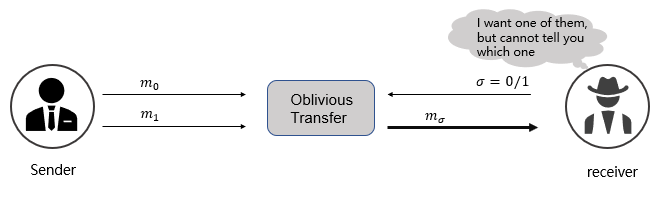
Oblivious Transfer is defined as the situation where the sender sends one single value from a set of values to the receiver. In such a way that the receiver does not know more than this single value, and the sender has no idea about which one he sends. Formally speaking, the sender knows $N$ values, and the receiver would like to get one value that its index is $i, 0\leq i<N$. When it's done, the receiver only knows $N_i$ without knowing $N_j$, where $j\neq i$, and the sender has no idea about $i$. This is the whole process of 1-out-of-N Oblivious Transfer.

As for $N=2$, $i.e.$ 1-out-of-2 Oblivious Transfer, the receiver inputs $\sigma = 0/1$ according to each bit of his input, the sender takes label $m0$,$m_1$ as input. Once OT finished executing, the receiver obtains label $m\sigma$. Figure 1 shows the process of 1-out-of-2 OT. During its whole process, the following properties are satisfied:

  • The sender does not know which label is chosen by the receiver.
  • The receiver has no idea about the another one $m_{1-\sigma}$.

Figure 1: 1-out-of-2 OT

Details of Secure Two-party Computation#

The workflow of secure two-party computation is:

Two computing parties Alice and Bob would like to jointly compute $f(s,t)$, where $s$ is the input data owned by Alice, $t$ is owned by Bob, $f$ is the computing logic. Firstly, Alice turns $f$ into the boolean circuit $C$, in which each gate has a truth table represents the input and output of it. Secondly, Alice encrypts the truth table to get the garbled circuit $\widetilde{C}$. Then Alice encrypts her input and sends the encrypted input and $\widetilde{C}$ to Bob. So Bob gets both $\widetilde{C}$ and the encrypted input of Alice - corresponding to his input label, but he cannot obtain his own encrypted input as without knowing how Alice's input is encrypted. Afterward, Bob can get them - corresponding to her input label by executing 1-out-of-2 OT with Alice. Finally, Bob takes two parties' encrypted input as the input to decrypt the garbled circuit $\widetilde{C}$, and obtains the output result.

The whole process can be divided into five steps, the details of which are shown below.

1. Generating boolean circuit#

Let $f(s,t)$ as the function to be computed securely, it can be represented as a boolean circuit $C$, satisfying $f(s,t)=C(s,t)$ for any $s,t$. Theoretically, any function can be represented as a boolean circuit, and its format is shown Figure 2.

Figure 2: representing function as boolean circuit

2. Generating garbled circuit#

After representing a function as boolean circuit $C$, Alice creates a truth table as shown in Figure 3 according to each gate in $C$, and then transforms this truth table into garbled circuit $\widetilde{C}$.

Figure 3: creating the truth table

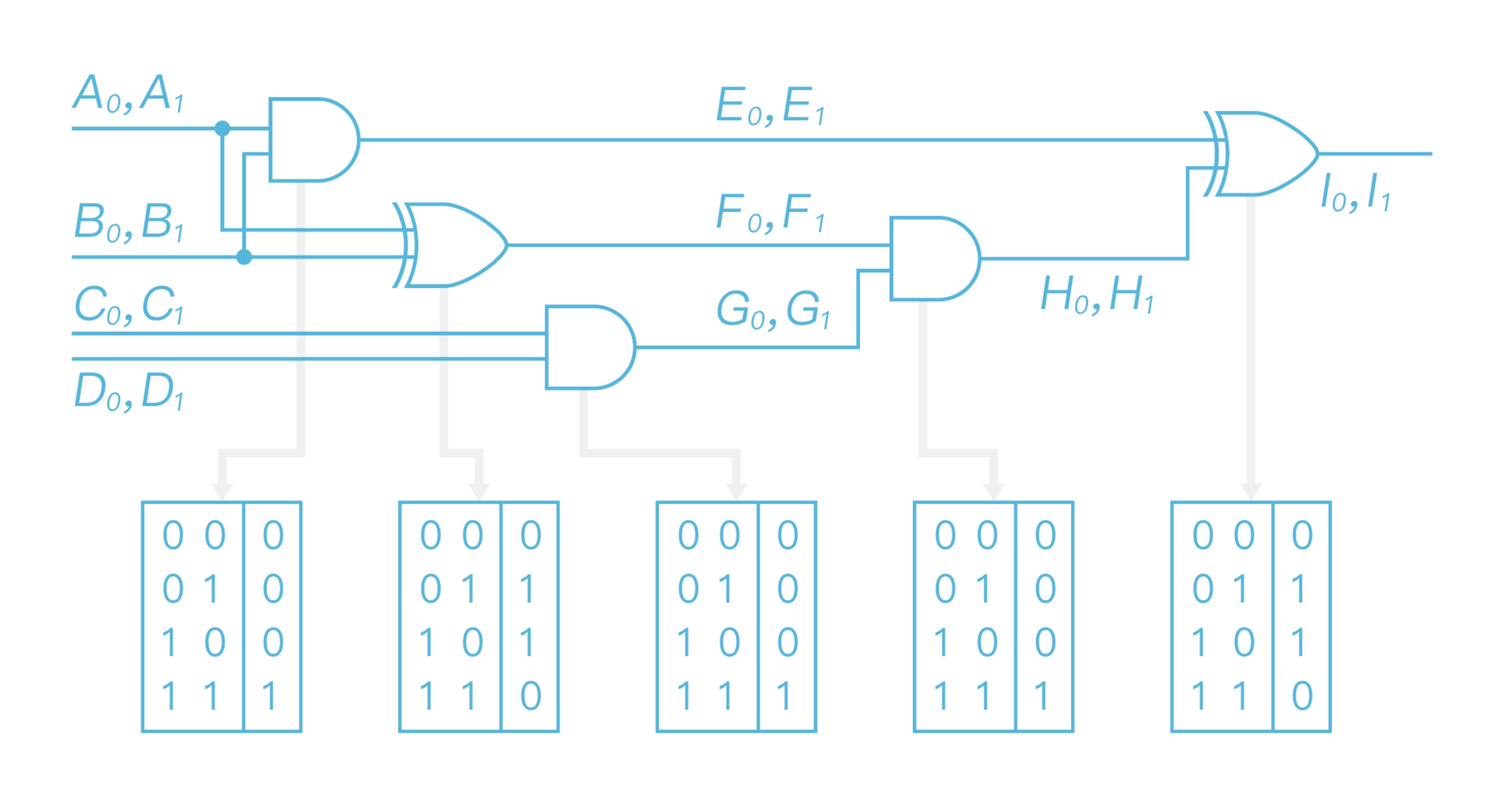
\ And then Alice chooses two random labels $A_0$ and $A_1$ in $k$ bit length for each wire to represent 0,1 respectively, where $k$ is the security parameter equals to 128 bits. For example, $A_0$ represents 0, $A_1$ represents 1, but this relationship is only known to Alice. Afterward, Alice replaces the whole circuit gate by gate. Taking the first two AND, XOR gates in Figure 3 as the example, the processes of replacing these two are shown as Figure 4.

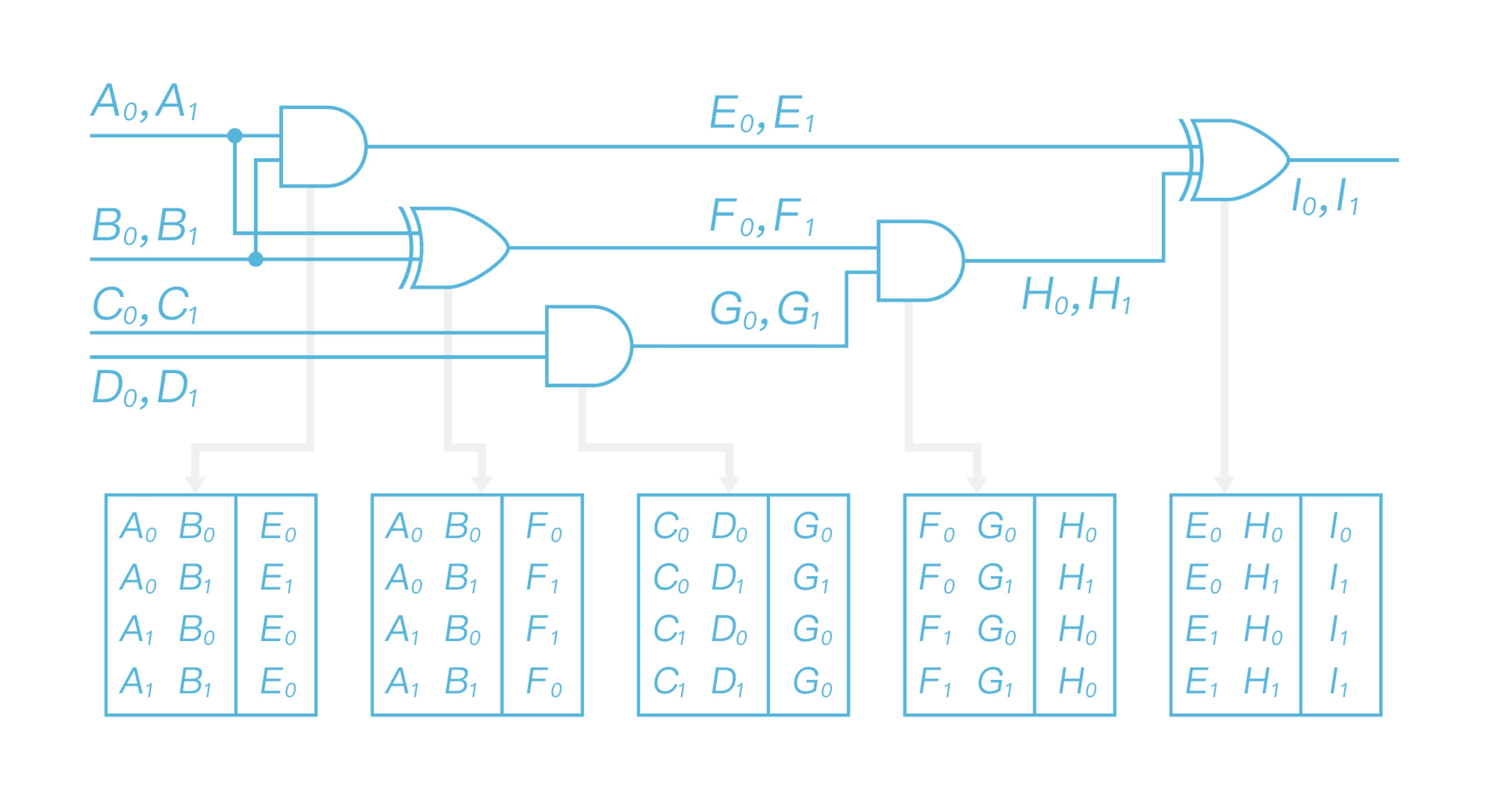
Figure 4: replacing 0/1 in truth table with lables

\ After finishing replacing all gates, the generated garbled circuit is shown as Figure 5.

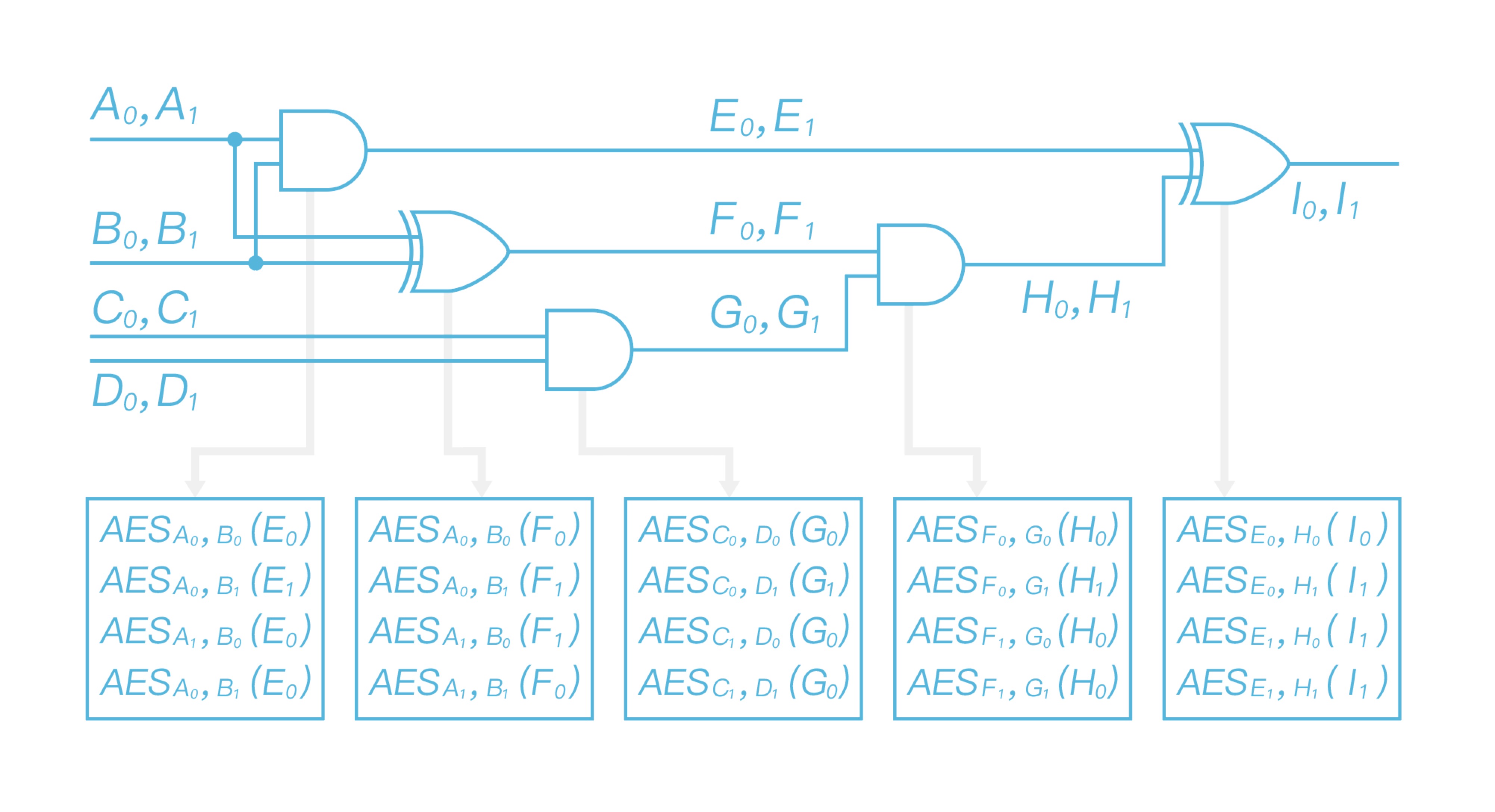
Figure 5: choosing random numbers to replace 0/1 gate by gate

\ Now that Alice uses two input labels to encrypt the output label gate by gate. Taking the first row in the first table as the example, Alice takes $A0$ and $B_0$ as the input to double AES encrypt output label $E_0$, and obtains $AES{A0}(AES{B_0}(E_0))$. All left gates in this circuit are processed the same way as the first one, after finishing processing all gates, it will get the garbled table as shown in Figure 6 and obtain the garbled circuit $\widetilde{C}$ eventually.

Figure 6: encryting output label with input labels

3. Sending Alice's label according to her input#

After generating the garbled circuit, Alice needs to encrypt her original input $s$. At first, she transforms $s$ into the boolean value corresponding to the input of $C$, then replaces each bit of the boolean value with $A_0$ and $A_1$ according to the input of $\widetilde{C}$. It will obtain the whole labels after replacing every bit. Afterward, Alice sends these labels and $\widetilde{C}$ to Bob together.

Let Alice's original input is $s=s_0s_1=10$, she sends labels $A_1$ and $B_0$to Bob according her input.

4. Receiving Bob's label according to his input#

Now that Bob has both garbled circuit $\widetilde{C}$ and Alice's label, in order to decrypt $\widetilde{C}$, he still need the labels corresponding to his input. As the encryption process demonstrated before, Alice knows Bob's input labels but has no idea about his original input. Bob knows his own original input but has no idea about his input label. Bob achieve it by using 1-out-of-2 OT with Alice bit by bit according to her original input, where Alice is the sender, Bob is the receiver, Bob inputs 0 or 1 according to his actual input. Afterward, he obtains his whole input label according to his input while Bob learns no additional information and Alice is not able to know Bob's original input.

Let Bob's original input is $t=t_0t_1=01$, after executing OT with Alice, he obtains $C_0$ and $D_1$ according his input. Then he is able to decrypt the garbled circuit by using both parties' input labels.

5. Evaluating the garbled circuit#

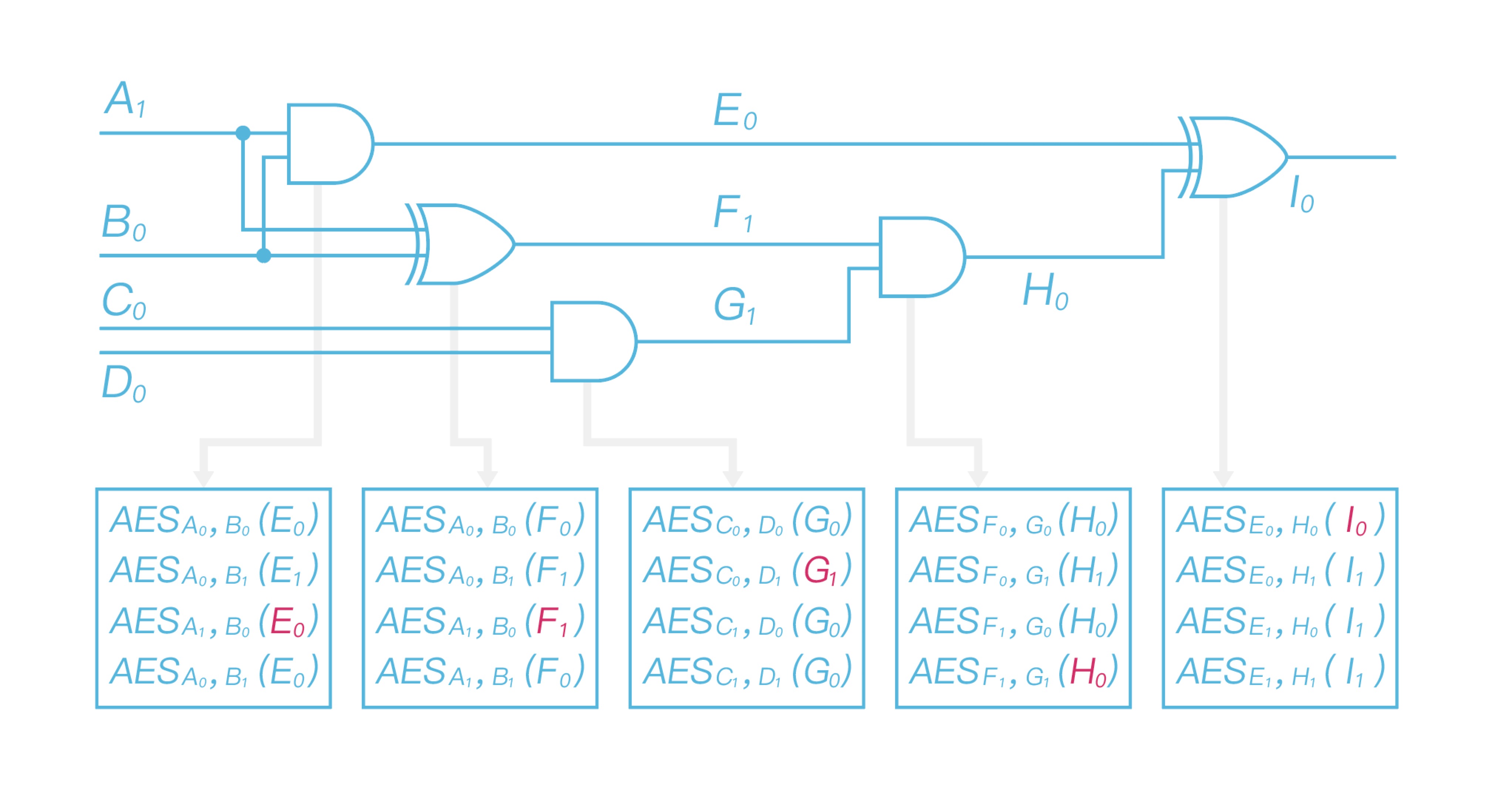
Bob now has already received the input labels corresponding to his original input, labels he owns are $A_1$, $B_0$, $C_0$ and $D_1$. Then he decrypts the garbled circuit gate by gate and delivers the output of each decrypted gate as the input to decrypt the next gate. After evaluating the garbled circuit, Bob obtains output label as shown in Figure 7.

As for the first garbled table, Bob takes $A_1$ and $B_0$ as decryption key to get $E_0$; As for the second garbled table, he takes $A_1$ and $B_0$ as decryption key to get $F_1$; As for the third garbled table, Bob takes $C_0$ and $D_1$ as decryption key to get $G_1$; As for the fourth garbled table, Bob takes $F_1$ and $G_1$ as decryption key to get $H_0$; At last, he takes $E_0$ and $H_0$ as decryption key decrypt the last garbled table, and obtain the final output label $I_0$. Since Bob knows its corresponding relationship with 0/1, he is able to get the computing result and send it to Alice. So both of them have the final output result.

Figure 7: decrypting gate by gate to obtain the output label

Paradigm of Secure Two-party Computation#

Figure 8: paradigm of secure two-party computation

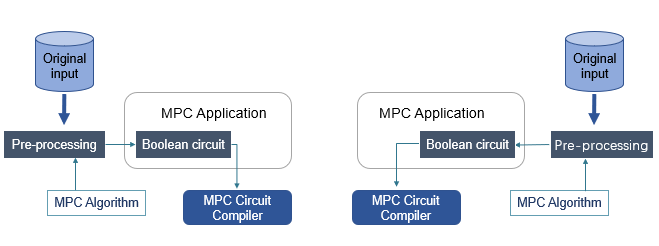
\ Figure 8 demonstrates an ordinary paradigm of secure two-party computation. The workflow is shown below.

  1. One of these two parties codes application algorithm by some common high-level programming languages, such as C++, Java, Python, etc. (depending on the MPC framework used)
  2. The Application algorithm will be compiled into the boolean circuit (consisting of AND, XOR and NOT gates) saved in a file by MPC Circuit Compiler.
  3. These two computing participants pre-process their own original input and transform them into the data format as the input of the boolean circuit.
  4. Both of them execute the boolean circuit by the installed MPC software and make the MPC computation.
  5. When MPC computation is done, both of them obtain the correct output result. Most importantly, it can be guaranteed that no more than the original input would be leaked.

Paradigm of MPC in PlatON#

MPC is one of the most important technologies used in PlatON, and secret contracts are implemented with MPC in PlatON, which can protect the privacy of original data belonging to each computing participant.

Figure 9 demonstrates the computing architecture of Secure Two-party Computation in PlatON.

Figure 9: Architecture of Secure Two-party Computation in PlatON

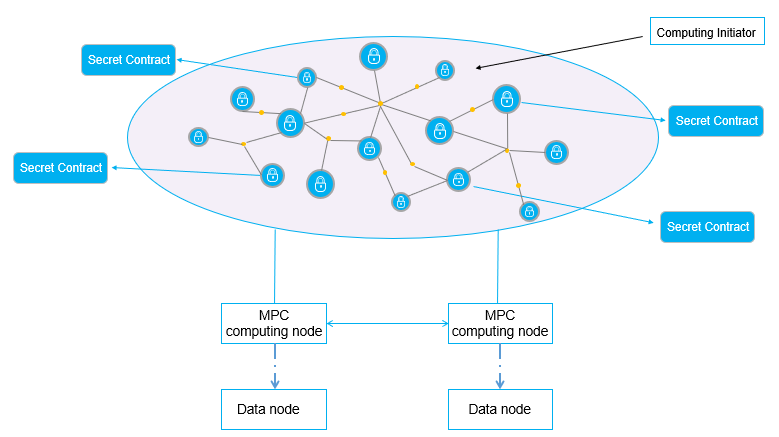
\ Programming of secret contracts in PlatON is compatible with high-level programming languages. Instead of being compiled into redundant boolean circuit file, secret contracts will be compiled into more efficient LLVM IRs. And then LLVM IRs will be deployed onto PlatON network to be executed by JIT in MPC-VM on computing nodes. Input data of secret contracts are kept by data nodes in local, while computing nodes do MPC computation off-chain, and publish the output result onchain.

Future plans#

PlatON will optimize the current implemented MPC architecture in order to extend it to more innovational and efficient MPC protocols. PlatON will improve it in the following several ways.

  • combining with homomorphic encryption (HE) to decrease the communication complexity fo MPC.
  • implementing three-party computation and more to satisfy more complex practical application scenarios.